Vector
What is a vector?
A vector is a directed line segment. It starts at a point called the tail and ends at a point called the head. The vector is described by the coordinates of these two points.
Here's the calculation of a vector AB(3,4) point from A(2,3) to B(5,7):
Vector magnitude
The magnitude of a vector is the length of the vector. It represents the distance from the vector's tail to its head.
Normalized vector
A normalized vector, also known as a unit vector, is a vector that has been scaled to have a magnitude of exactly 1, while maintaining its direction.
Normalized vector often used as a direction vector. Ex: describing direction of forces or velocities in physics or defining orientations in graphics.
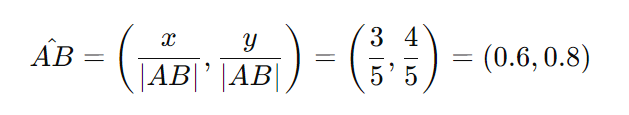
Absolute vector
An absolute vector represents the position of a point in a coordinate system relative to the origin (0, 0). It describes the point's location in the coordinate space without reference to any other point.
Here's the calculation of an absolute vector of point A(1,3)
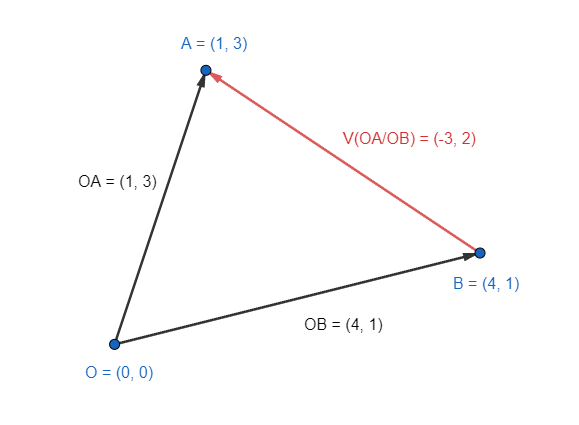
Relative vector
A relative vector represents the position of a point in a coordinate system relative to another point. It describes the point's location in the coordinate space with reference to another point.
In the definition of vector AB(3,4) point from A(2,3) to B(5,7), AB is a relative vector of point A and B.
Relative velocity
Relative velocity describes the velocity of one object relative to another, effectively describing how fast one object is moving relative to the other. It is determined by subtracting a velocity vector from another.
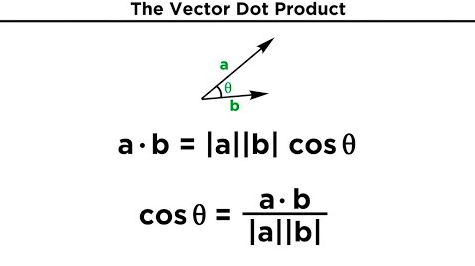
Dot product
The dot product (also known as the scalar product) is an operation that takes two vectors and returns a single scalar value.
Here's the calculation of the dot product of vectors OA(1,3 and OB(4,1)
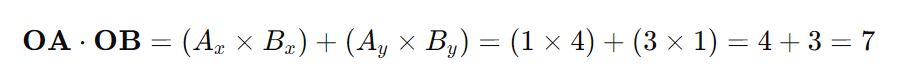
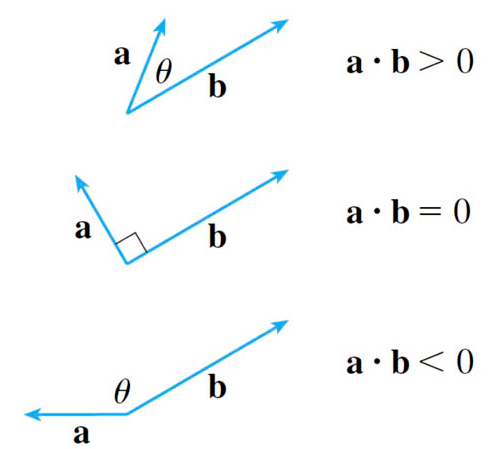
Some applications of the dot product in vector math:
- Find angle between two vectors
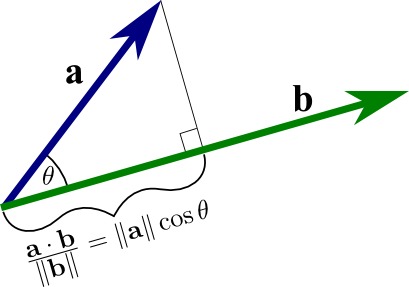
- Projection of Vectors
- Orthogonality